The JPEGs
The images
The IP camera generates JPEG encoded images that superficially look like a slightly greenish rectangle of 640 x 480 pixels (VGA):-

Exactly what the camera sees.
The webcam is intact bar the IR illuminator having been disabled. There were plans to remove the camera lens in the future to get an even more uniform light distribution on the CMOS sensor.
If the image has graphic equalisation performed on it, a captured frame looks like (when zoomed in):-

Close up of exactly what the camera sees.
or (with animation of multiple frames):-
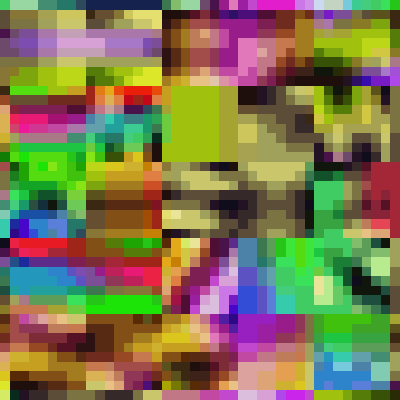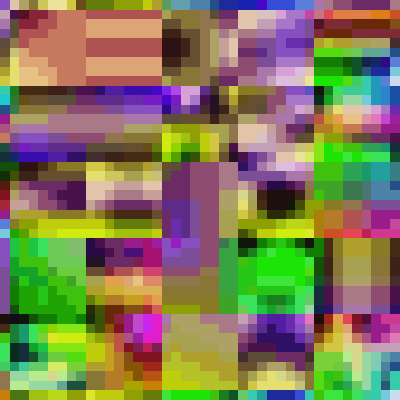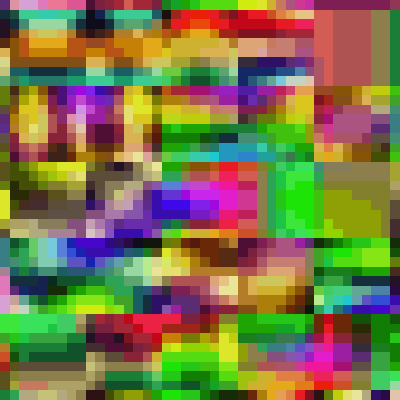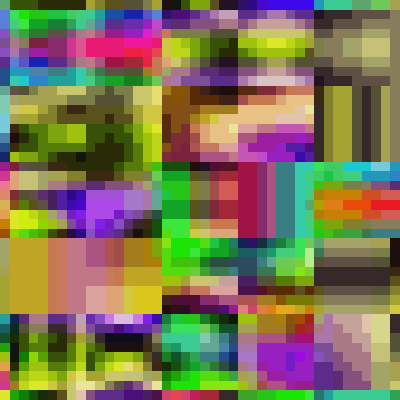
Animation and close up of exactly what the camera sees.
The coloured squares show the pixel distribution across a small part of the JPEG. This section has been equalised to emphasise the per pixel variations. This equalisation does not affect the images’ entropy content, it’s just a trick to help with visualisation. The variations appear totally random (within the context of the JPEG algorithm that produced the image). The 8 x 8 pixel sub images are a typical characteristic of the block splitting that occurs in all JPEG images when minimum coded units (MCUs) are created. The patterns within an MCU represent the two dimensional discrete cosine transform (DCT) of that part of the image. DCT and it’s quantization contribute to the lossy nature of JPEG compression. The pattern itself is not the entropy that we are looking for. For the interested, an archive of frames is available below for download and inspection.
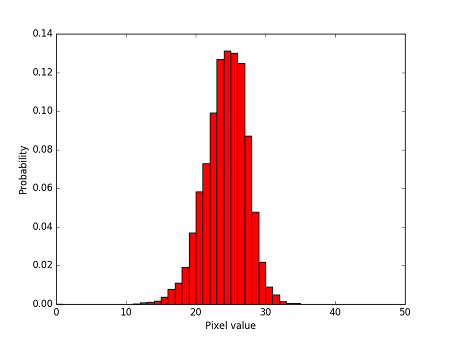
The files are generated with the following size distribution (over 10,000 frames), and this sets the expectation for what we will have to work with for entropy extraction. The temperature within the integrating sphere was 36oC, which is approximately 7oC above ambient. This is the expected temperature rise from the camera’s 2.75W power consumption, and the mean file sizes are correlated with the temperature inside the sphere.
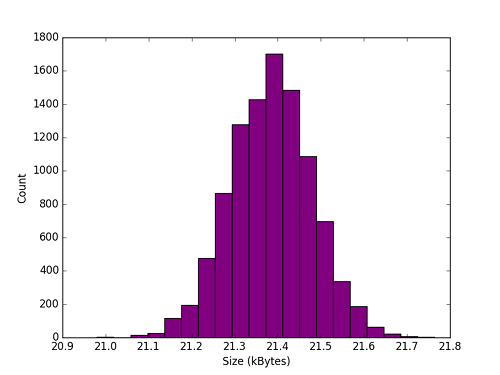
Distribution of JPEG sizes.
Noise origins
The camera uses a CMOS sensor that looks like this below. The lens has been removed to expose the sensor for the photograph, but is in place during operation.

Exposed CMOS sensor.
The entropy arises from temporal and fixed pattern noises such as:-
- Photon noise (a Poisson process)
- Clock noise (related to $\sqrt{f}$)
- Noise in dark current (Gaussian and Poisson distributions as a result of semiconductor impurities)
- Flicker noise (related to sensor sample frequency by $ \frac{1}{f} $)
- Johnson–Nyquist noise (temperature dependant Gaussian distribution)
- Quantization noise (uniformly distributed between $- \frac{1}{2} $ lsb and $+ \frac{1}{2} $ lsb of the sensors analogue to digital converter)
Other noise enters the JPEG file due to the lossy processing algorithm. Discrete cosine transformation and subsequent floating point quantization adds further unpredictable entropy to the output files.
Analysis
Taking any particular Photonic frame, we get the following three channel histogram, the combined RGB histogram using our Entropy Inspector application and summary statistics of (expected) normal distributions:-
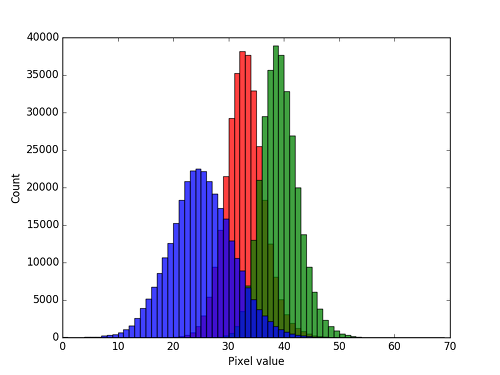
Typical frame decomposed into red, green and blue channel histograms.
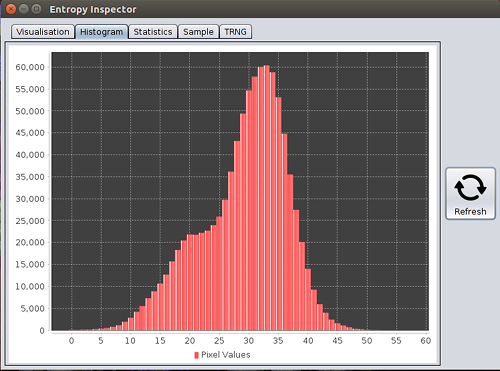
Combined histogram of a typical frame.
Summary statistics for many frames:-
| Channel | Mean ($ \mu $) | Standard deviation ($ \delta $) | Signal to noise ratios (SNR) ,dB |
|---|---|---|---|
| red | 32.1 | 3.32 | 13.5 |
| green | 37.2 | 3.31 | 14.3 |
| blue | 23.8 | 5.87 | 10.1 |
| combined RGB | 32.2 | 7.24 | 13.2 |
<0.003% of all pixels clip to black
The higher pixel values for the green channel explain the green tint to the images. Since all of the photodetectors constituting the CMOS sensor are identical and the illumination is pure white, we can attribute the spectral shift away from neutral grey to the JPEG algorithm.
The other observable point is $ \mu $. A $ \mu $ of 32.2 is approximately 25% of the way to mid grey (pixel value = 127). This is confirmation that the webcam’s auto exposure function has been unable to compensate for the very low illumination. This failing works to our advantage in minimising the SNR, and therefore maximising sensor noise. The entropy signal within a frame is therefore 13.2dB using the 20log rule, with blue as the most entropic channel.
In the far, far future when the moon has fallen back to Earth and Morlocks rule the land, we might optimise the potential entropy rate by reducing the illumination within the integrating sphere. There is clearly a sweet spot where $ \mu_{RGB} $ could be left shifted which would probably increase the width ($ \delta_{RGB} $) of the combined histogram, even though more clipping to zero would occur. Sigh.
Are the JPEGs indeed random?
We captured 330,000 frames during an experiment. Each JPEG file was SHA1 hashed, and the resultant 160 bit hash strings histogrammed. There was only one count against each hash string. The strong speculation is that each JPEG file was unique. Assuming they are all independent, we can apply the Birthday Problem in reverse to approximate how many files would be needed for this many to be unique, given a certain confidence value $\alpha$ as:-
$$ -\frac{k^2}{2N} \gt \log(1-\alpha) $$
implying
$$ N \gt\frac{-k^2}{2\log(1-\alpha)} \approx \frac{k^2}{2\alpha}=N^{*} $$
for small $\alpha$. With $k$=330,000-1 and $\alpha$=0.05 (corresponding to 95% confidence), $N \gt 10^{12}$. That’s a trillion possible JPEGs at least, given that 330,000 of them were unique. Or three times the number of stars in our galaxy. Randomish then, but no evidence to support the hypothesis that the frames are not random.
(Thanks to whuber for assistance with the probabilities.)
Due to the extent of variability between JPEG files, we go out on a proverbial limb and posit that all original JPEG files are unique. We mean all unique in the world. We mean all photos taken throughout the land, by all devices are unique, even if they look the same to the unaided eye.
Try it. Put a camera on a timer and take several identical shots. Then hash them and compare the hash values. They will all be different. We (almost) guarantee it. And what of EXIF data we hear you ask? The webcam we use is a simple (read cheap) model, and does not embed EXIF data, so there is no incremental timestamp to be uniquely hashed. The ever present random sensor noise creates a slightly different version of any fixed scene. And the resultant JPEG encapsulates that variance.
A further illustration of the variability of the JPEGs can be shown using Kullback–Leibler (KL) divergence from one frame’s byte distribution to the next. The graph shows the divergence between two pairs of consecutive frames in accordance with:-
$$ D_{KL}(f_{n+1}|f_{n}) = \sum_{i} f_{n+1}(i) \enspace \log_2 \frac{f_{n+1}(i)}{f_{n}(i)} $$
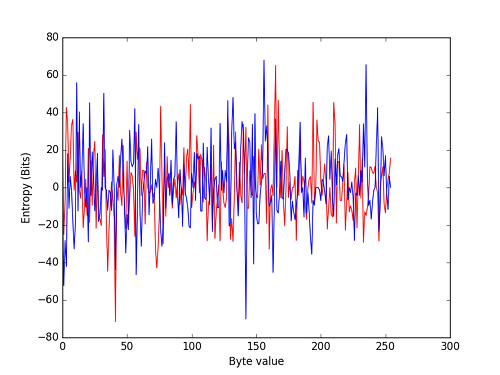
Two KL divergences based on four JPEGs, for all $i$
Blue is one pair of consecutive frames, and red the other. The two traces are very different as expected. One trace is sufficient, but it could lead to the incorrect conclusion that each subsequent frame’s entropy diverges by the same amount. In reality they diverge by normally distributed positive and negative amounts, with a $\mu_{KL}$ of 0 centred upon a mean file size of ~21.4kB.
Final proof of randomness
And finally, evidence for randomness comes from considering one single photo-sensor site in the webcam’s array. The following is exactly the Gaussian jitter we’d expect on a single red sensor in the middle of the image subject to random noise :-