Poor randomness looks like...
We thought that it might useful to illustrate what ‘poor’ randomness actually looks like, rather than just trying to quantify it statistically /quantitatively. Not many people have seen this.
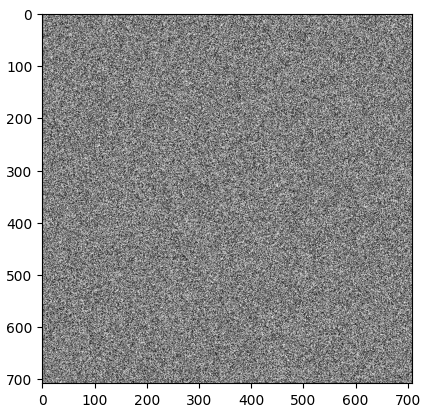
Perfectly good randomness used for masking.
So we took a couple of test images (some terrible RANDU output and the famous Lena). The original image rasters (with pixels at $[i, j]$ coordinates) were then masked by the image above as:-
testImage[i, j] = image[i, j] ^ round(OPACITY * mask[i, j])
where OPACITY is an ersatz transparency coefficient. This allowed the image entropy to be gradually and linearly increased to 8 bits/byte (100%) as OPACITY $\to$ 1. $\text{max} (\delta \text{OPACITY} = 0.01) \equiv 2.56 $ pixel value. The following were generated with OPACITY = 0.96:-
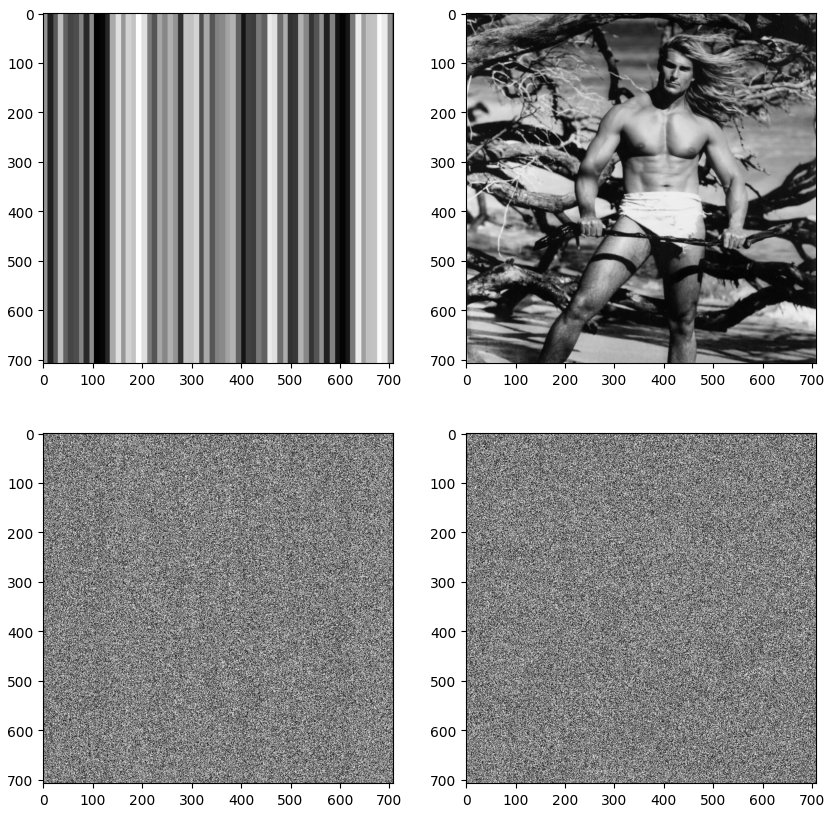
Test images masked with full entropy where OPACITY = 0.96.
giving a p value of 0.00103. That’s just a wee bit above the critical $\alpha$ value of 0.001 for the Sanity test. Perhaps you can just discern Lena’s loin cloth in some lights when you squint. The bars of the RANDU generator are slighter more distinguishable. That’s what poor randomness looks like. Testing these two images with ent and ent3000 gives:-
Entropy = 7.999117 bits per byte.
Optimum compression would reduce the size
of this 501264 byte file by 0 percent.
Chi square distribution for 501264 samples is 614.25, and randomly
would exceed this value less than 0.01 percent of the times.
Arithmetic mean value of data bytes is 127.2773 (127.5 = random).
Monte Carlo value for Pi is 3.137843532 (error 0.12 percent).
Serial correlation coefficient is 0.001615 (totally uncorrelated = 0.0).ent3000 starting...
--help option to display this help.
Testing first 500000 bytes.
Sane sample file. Good.
------------------------------------
Entropy, OoC, FAIL.
Compression, p = 0.393, PASS.
Chi, p = 0.467, PASS.
Mean, p = 0.037, FAIL.
Pi, p = 0.660, PASS.
UnCorrelation, p = 0.229, PASS.
------------------------------------
Finished.As far as ent3000 is concerned, we got an Out of Calibration /FAIL message for the Entropy test, and a FAIL for the Mean test.