1. Stable source

Golden Equation 1 - stability at a constant temperature

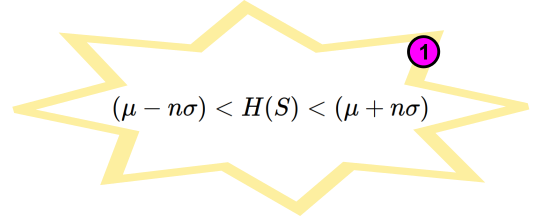
Otherwise, you’ll never manage to measure the entropy accurately! $\mu$ is the mean entropy ($H$) of your samples ($S$) and $\sigma$ is their standard deviation. We’ll discuss $n$ later. Clearly you will need to repeat the entropy measurement on multiple samples to obtain a mean and standard deviation. We suggest using ten samples taken over say an entire day /weekend. More samples will be more accurate of course but you need to be pragmatic. Then at any time in the future (at this temperature of course), you should expect the (Shannon) entropy to be within $\pm n \sigma$.

For Golden Rule 1 it is sufficient to focus on Shannon entropy, rather than the min. entropy that will be needed later.

So make sure that your entropy source is stable, both in the short and long term. That means ergotic and stationary. This is key. By stability, we don’t mean invariance to temperature effects but that is certainly a factor. We mean don’t try to use sources like atmospheric noise, raindrops, wired up chaotic jerk functions, aquarium fish or Chua circuits. These sources are not stable day to day /hour to hour, making their entropy rates indeterminate. The Chua circuit will require constant tweaking of variable components and atmospheric noise is more likely to be Lady Gaga’s latest or a passing police car. Similarly, floating analogue to digital converter pins are unreliable and very susceptible to the weather (humidity) or wandering paws.

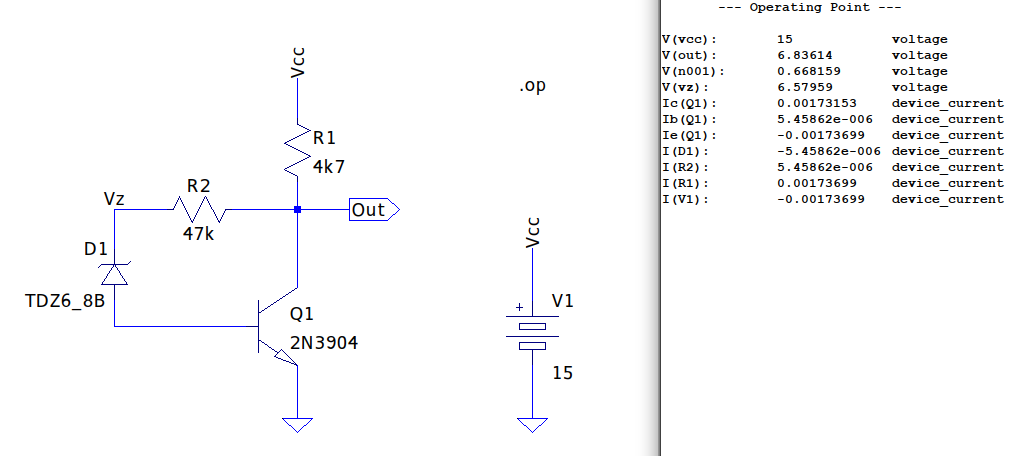
Reverse biased transistor instability

The clichéd reverse biased transistor also falls into the don’t use category. Electrical ageing effects rapidly accumulate with $V_{BE}$ as low as -8V[1]. For example the common USB form factor ChaosKey TRNG drives 2N3904 transistors at $-20V_{BE}$. Ouch! Other USB format devices operate at similar relatively high reverse voltages. The damage can manifest itself as long term noise drift. Exactly the type of problem repeatedly experienced by Rob Seward with his early TRNG designs (driven at $-12V_{BE}$).

Conventional transistor instability

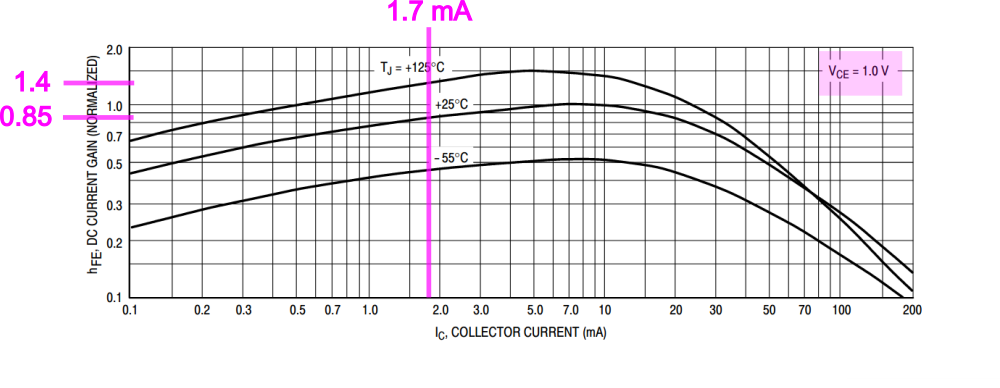
Even transistors in conventional forward bias still require nuanced usage. This is a problem as a lot of entropy circuit designs incorporate them. Without some careful biasing and temperature compensation, their current gain ($h_{FE}$) is somewhat indeterminate. Our Mata Hari and Dangerous Box designs use them solely as voltage followers which is kinda okay as that makes the circuit $h_{FE}$ agnostic.

Expand boring technical details of conventional transistor instability:-

The above circuit exhibits an $I_C$ of 1.7 mA for a typical $V_{CC}$ of 15V. And a $h_{FE}$ of 317 (from an LT Spice simulation and tallies with the data sheet's maximum of 400 at $I_C = 1$ mA). From ON Semiconductor's version of the venerable 2N3904 small signal transistor:-

Which inevitably leads us to the following appropriate chart:-

But $V_{CE}$ is actually 6.8V in the above circuit, and there is no data available for that level of collector emitter voltage. Skipping over that, we see that the transistor's current gain increases by approximately 64% over the +25 °C to +125 °C temperature range. Wobbly! Which is why you need to measure the entropy rate at minimum and maximum likely temperatures.

And thus:-

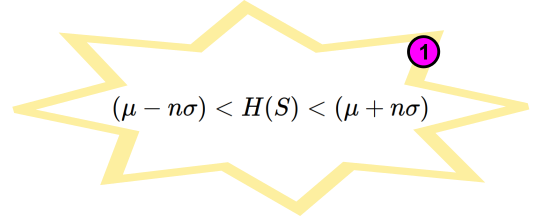
In the first Golden Equation we suggest $n = 3.3$. Weird choice, eh? If we assume 😯 a Normal distribution via the central limit theorem for $H(S)$, $ \pm 3.3 \sigma$ means that $p=0.001$ of an alarm condition occurring by chance. I.e. the entropy source drifting too far to be accurately measured and relied upon. That’s equivalent to common randomness test suite thresholds.

So how to determine how much entropy you have? We suggest using the super duper compressor cmix from here if you have the hardware. Otherwise use whatever compression you have to hand (7Zip, PKZip e.t.c.) Compress sample files and the resultant size should be indicative of the files’ entropy. Of course this technique is mathematically doomed to overestimate $H$, but the ratios of the various samples will be a very good indicator of the source’s stability.

References:-

[1] N. Toufik, F. Pilanchon and P. Mialhe, Degradation of junction parameters of an electrically stressed npn bipolar transistor, c.e.f., University of Perpignan, 52 av. de Villeneuve, F-66860 Perpignan.