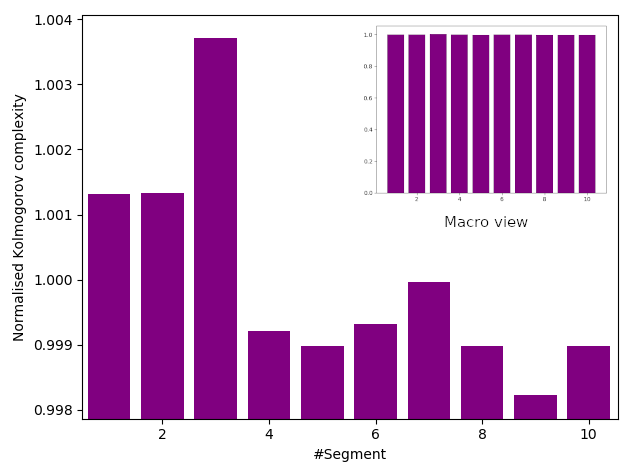
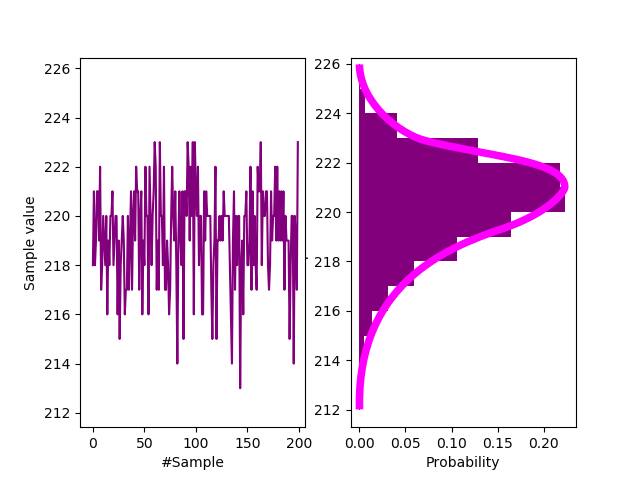
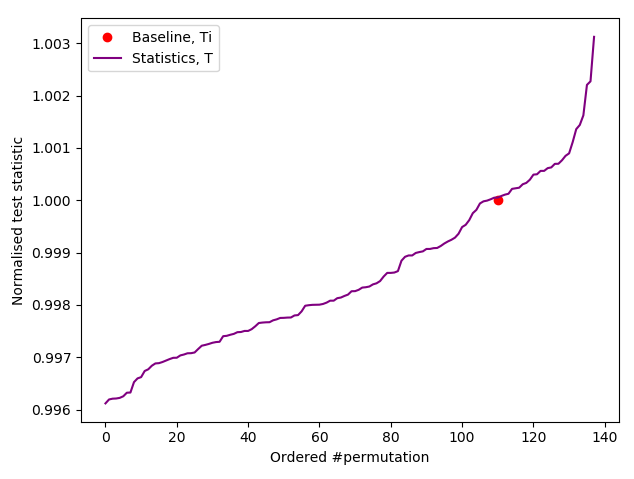
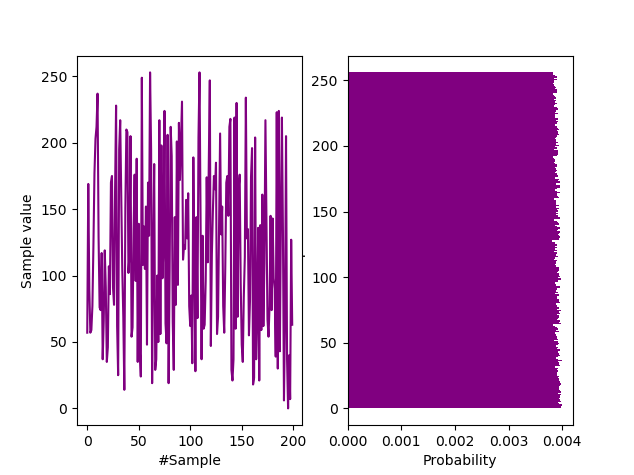
$ java -jar "iid-tester.jar" /tmp/mata-hari-1mb-x1bit.bin /tmp/results.json
Starting IID test...
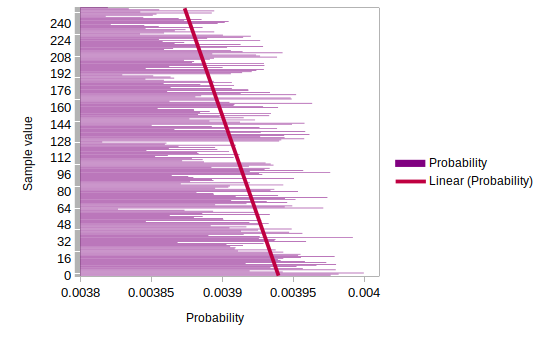
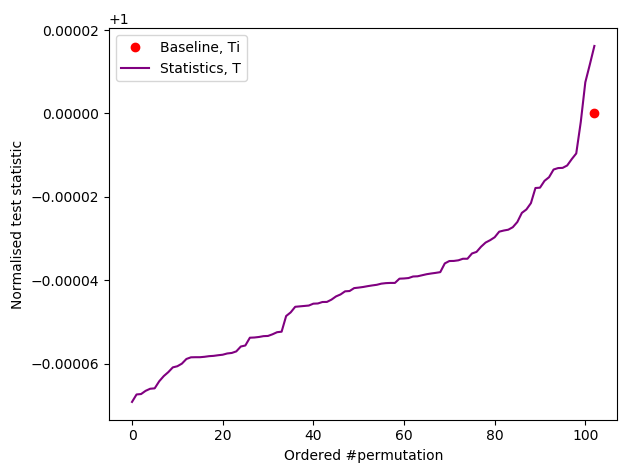
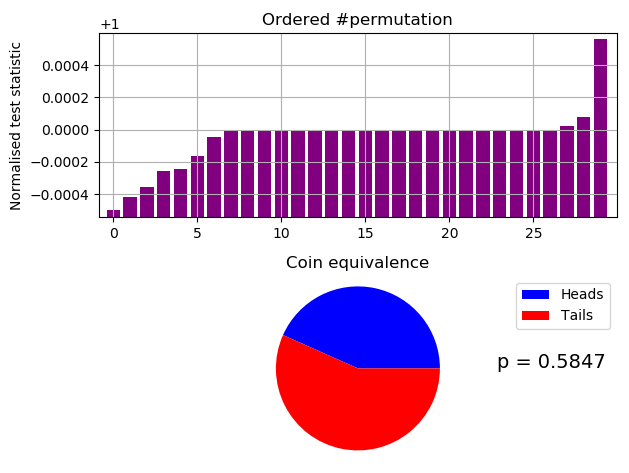
Baseline: 587677
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Compressor Thread-0 started.
Compressor Thread-3 started.
Compressor Thread-1 started.
Compressor Thread-4 started.
Compressor Thread-2 started.
Compressor Thread-1 Permutation 1, Normalised statistic = 0.9969881414450454
Compressor Thread-4 Permutation 1, Normalised statistic = 0.9976670858311624
Compressor Thread-3 Permutation 1, Normalised statistic = 0.9961169145636123
Compressor Thread-0 Permutation 1, Normalised statistic = 0.9970749238101883
Compressor Thread-2 Permutation 1, Normalised statistic = 0.997983586221683
Compressor Thread-1 Permutation 2, Normalised statistic = 0.9959790837483856
Compressor Thread-4 Permutation 2, Normalised statistic = 0.9961917856237354
Compressor Thread-3 Permutation 2, Normalised statistic = 1.0002178067203582
Compressor Thread-0 Permutation 2, Normalised statistic = 0.9985417159426011
Compressor Thread-2 Permutation 2, Normalised statistic = 1.0003930730656465
Compressor Thread-1 Permutation 3, Normalised statistic = 0.9989194744732225
Compressor Thread-4 Permutation 3, Normalised statistic = 1.0013595903872365
Compressor Thread-2 Permutation 3, Normalised statistic = 0.9996205398543758
Compressor Thread-3 Permutation 3, Normalised statistic = 0.9974816097958572
Compressor Thread-0 Permutation 3, Normalised statistic = 0.9992853216988243
CURRENT RANK = 12
Remaining running time to full completion = 6672s
Estimated full completion date/time = 2020-12-17T22:45:25.671464
Compressor Thread-1 Permutation 4, Normalised statistic = 0.9990692165934688
Compressor Thread-4 Permutation 4, Normalised statistic = 1.0011111545968279
Compressor Thread-3 Permutation 4, Normalised statistic = 1.000049346835081
Compressor Thread-2 Permutation 4, Normalised statistic = 0.9974084403507368
Compressor Thread-0 Permutation 4, Normalised statistic = 0.9990879343584996
Compressor Thread-1 Permutation 5, Normalised statistic = 0.9980805782768426
Compressor Thread-4 Permutation 5, Normalised statistic = 0.9980805782768426
Compressor Thread-2 Permutation 5, Normalised statistic = 0.9977504649662995
Compressor Thread-0 Permutation 5, Normalised statistic = 1.0022052930436276
Compressor Thread-3 Permutation 5, Normalised statistic = 0.9962224146937859
Compressor Thread-1 Permutation 6, Normalised statistic = 0.9975020291758908
Compressor Thread-4 Permutation 6, Normalised statistic = 0.9986114821577159
Compressor Thread-0 Permutation 6, Normalised statistic = 0.9963211083639483
Compressor Thread-2 Permutation 6, Normalised statistic = 0.9986114821577159
Compressor Thread-3 Permutation 6, Normalised statistic = 0.9986182886177271
CURRENT RANK = 24
Remaining running time to full completion = 6662s
Estimated full completion date/time = 2020-12-17T22:45:25.671464
Compressor Thread-1 Permutation 7, Normalised statistic = 1.0004900651208062
Compressor Thread-4 Permutation 7, Normalised statistic = 0.9983375221422652
Compressor Thread-0 Permutation 7, Normalised statistic = 0.9989449986982645
Compressor Thread-3 Permutation 7, Normalised statistic = 0.9977572714263108
Compressor Thread-2 Permutation 7, Normalised statistic = 1.0006142830160105
Compressor Thread-1 Permutation 8, Normalised statistic = 0.9979937959116998
Compressor Thread-4 Permutation 8, Normalised statistic = 1.0005615329509236
Compressor Thread-2 Permutation 8, Normalised statistic = 0.9991253698885613
Compressor Thread-3 Permutation 8, Normalised statistic = 0.9980040056017165
Compressor Thread-0 Permutation 8, Normalised statistic = 0.997034085050121
Compressor Thread-1 Permutation 9, Normalised statistic = 0.9976687874461652
Compressor Thread-4 Permutation 9, Normalised statistic = 0.9992444829387572
Compressor Thread-3 Permutation 9, Normalised statistic = 1.0006278959360329
Compressor Thread-0 Permutation 9, Normalised statistic = 0.9974782065658516
Compressor Thread-2 Permutation 9, Normalised statistic = 0.9981282234969209
CURRENT RANK = 35
Remaining running time to full completion = 6652s
Estimated full completion date/time = 2020-12-17T22:45:25.671464
Compressor Thread-1 Permutation 10, Normalised statistic = 0.9990232729883933
Compressor Thread-4 Permutation 10, Normalised statistic = 1.0002280164103752
Compressor Thread-3 Permutation 10, Normalised statistic = 0.9977045213612239
Compressor Thread-0 Permutation 10, Normalised statistic = 0.9968809396998691
Compressor Thread-2 Permutation 10, Normalised statistic = 0.9977521665813023
Compressor Thread-1 Permutation 11, Normalised statistic = 0.9981962880970329
Compressor Thread-3 Permutation 11, Normalised statistic = 0.9967686331096844
Compressor Thread-4 Permutation 11, Normalised statistic = 0.997661980986154
Compressor Thread-2 Permutation 11, Normalised statistic = 0.9971566013303226
Compressor Thread-0 Permutation 11, Normalised statistic = 1.0008491058863969
Compressor Thread-1 Permutation 12, Normalised statistic = 0.9983307156822541
Compressor Thread-4 Permutation 12, Normalised statistic = 0.9963245115939539
Compressor Thread-2 Permutation 12, Normalised statistic = 0.9982626510821421
Compressor Thread-0 Permutation 12, Normalised statistic = 1.0003062907005038
Compressor Thread-3 Permutation 12, Normalised statistic = 0.9999931935399888
CURRENT RANK = 47
Remaining running time to full completion = 6642s
Estimated full completion date/time = 2020-12-17T22:45:25.671464
Compressor Thread-1 Permutation 13, Normalised statistic = 1.0001242178952043
Compressor Thread-4 Permutation 13, Normalised statistic = 0.9972944321455494
Compressor Thread-0 Permutation 13, Normalised statistic = 0.9981401348019405
Compressor Thread-2 Permutation 13, Normalised statistic = 0.9982609494671393
Compressor Thread-3 Permutation 13, Normalised statistic = 0.9991730151086397
Compressor Thread-1 Permutation 14, Normalised statistic = 0.9974458758807985
Compressor Thread-4 Permutation 14, Normalised statistic = 0.9974016338907257
Compressor Thread-2 Permutation 14, Normalised statistic = 0.9977232391262547
Compressor Thread-0 Permutation 14, Normalised statistic = 0.998043142746781
Compressor Thread-3 Permutation 14, Normalised statistic = 0.9977981101863779
Compressor Thread-1 Permutation 15, Normalised statistic = 0.9972535933854821
Compressor Thread-4 Permutation 15, Normalised statistic = 0.9967363024246312
Compressor Thread-3 Permutation 15, Normalised statistic = 0.9972195610854262
Compressor Thread-0 Permutation 15, Normalised statistic = 0.9966188909894381
Compressor Thread-2 Permutation 15, Normalised statistic = 0.9959790837483856
CURRENT RANK = 61
Remaining running time to full completion = 6632s
Estimated full completion date/time = 2020-12-17T22:45:25.671464
Compressor Thread-1 Permutation 16, Normalised statistic = 1.0022733576437397
Compressor Thread-4 Permutation 16, Normalised statistic = 1.0002399277153946
Compressor Thread-2 Permutation 16, Normalised statistic = 0.997076625425191
Compressor Thread-0 Permutation 16, Normalised statistic = 0.9970511012001491
Compressor Thread-3 Permutation 16, Normalised statistic = 0.9990096600683709
Compressor Thread-1 Permutation 17, Normalised statistic = 1.0006976621511476
Compressor Thread-4 Permutation 17, Normalised statistic = 0.9983919738223548
Compressor Thread-3 Permutation 17, Normalised statistic = 0.9984123932023884
Compressor Thread-2 Permutation 17, Normalised statistic = 0.998000602371711
Compressor Thread-0 Permutation 17, Normalised statistic = 0.9982881753071841
Compressor Thread-1 Permutation 18, Normalised statistic = 1.000695960536145
Compressor Thread-0 Permutation 18, Normalised statistic = 0.9975020291758908
Compressor Thread-4 Permutation 18, Normalised statistic = 0.9983511350622876
Compressor Thread-3 Permutation 18, Normalised statistic = 0.9994878138841574
Compressor Thread-2 Permutation 18, Normalised statistic = 0.997289327300541
CURRENT RANK = 72
Remaining running time to full completion = 6622s
Estimated full completion date/time = 2020-12-17T22:45:25.671464
Compressor Thread-0 Permutation 19, Normalised statistic = 0.9969081655399139
Compressor Thread-1 Permutation 19, Normalised statistic = 1.0016233407126705
Compressor Thread-3 Permutation 19, Normalised statistic = 0.9981707638719909
Compressor Thread-2 Permutation 19, Normalised statistic = 0.9990692165934688
Compressor Thread-4 Permutation 19, Normalised statistic = 1.0004968715808173
Compressor Thread-1 Permutation 20, Normalised statistic = 0.9968860445448775
Compressor Thread-0 Permutation 20, Normalised statistic = 1.0001072017451764
Compressor Thread-2 Permutation 20, Normalised statistic = 0.9970902383452135
Compressor Thread-4 Permutation 20, Normalised statistic = 0.9974288597307704
Compressor Thread-3 Permutation 20, Normalised statistic = 0.9962105033887663
Compressor Thread-1 Permutation 21, Normalised statistic = 1.000051048450084
Compressor Thread-0 Permutation 21, Normalised statistic = 0.9965950683793989
Compressor Thread-4 Permutation 21, Normalised statistic = 0.999084531128494
Compressor Thread-3 Permutation 21, Normalised statistic = 0.9988446034130993
Compressor Thread-2 Permutation 21, Normalised statistic = 0.9962071001587607
Compressor Thread-1 Permutation 22, Normalised statistic = 0.9962530437638363
CURRENT RANK = 84
Remaining running time to full completion = 6549s
Estimated full completion date/time = 2020-12-17T22:44:22.671464
Compressor Thread-2 Permutation 22, Normalised statistic = 1.0000816775201344
Compressor Thread-3 Permutation 22, Normalised statistic = 0.9969370929949615
Compressor Thread-4 Permutation 22, Normalised statistic = 0.9975905131560364
Compressor Thread-0 Permutation 22, Normalised statistic = 0.9997532658245941
Compressor Thread-1 Permutation 23, Normalised statistic = 0.9969643188350064
Compressor Thread-2 Permutation 23, Normalised statistic = 0.9986455144577718
Compressor Thread-3 Permutation 23, Normalised statistic = 0.9968366977097963
Compressor Thread-0 Permutation 23, Normalised statistic = 0.9978763844765066
Compressor Thread-4 Permutation 23, Normalised statistic = 0.9999795806199664
Compressor Thread-1 Permutation 24, Normalised statistic = 1.0008967511064752
Compressor Thread-2 Permutation 24, Normalised statistic = 0.9975360614759469
Compressor Thread-3 Permutation 24, Normalised statistic = 1.0000187177650308
Compressor Thread-0 Permutation 24, Normalised statistic = 1.0005615329509236
Compressor Thread-4 Permutation 24, Normalised statistic = 0.9989449986982645
Compressor Thread-1 Permutation 25, Normalised statistic = 0.997804916646389
Compressor Thread-2 Permutation 25, Normalised statistic = 1.0003318149255458
Compressor Thread-3 Permutation 25, Normalised statistic = 0.9998162255796977
Compressor Thread-4 Permutation 25, Normalised statistic = 0.9965236005492814
Compressor Thread-0 Permutation 25, Normalised statistic = 0.9995303542592274
CURRENT RANK = 98
Remaining running time to full completion = 6335s
Estimated full completion date/time = 2020-12-17T22:40:58.671464
Compressor Thread-1 Permutation 26, Normalised statistic = 0.9993601927589475
Compressor Thread-2 Permutation 26, Normalised statistic = 1.0007640251362568
Compressor Thread-0 Permutation 26, Normalised statistic = 0.9972757143805185
Compressor Thread-3 Permutation 26, Normalised statistic = 1.0031241651451392
Compressor Thread-4 Permutation 26, Normalised statistic = 0.999212152253704
Compressor Thread-1 Permutation 27, Normalised statistic = 0.9972348756204513
Compressor Thread-2 Permutation 27, Normalised statistic = 0.9969898430600483
Compressor Thread-3 Permutation 27, Normalised statistic = 0.998017618521739
Compressor Thread-0 Permutation 27, Normalised statistic = 1.001439566292368
Compressor Thread-4 Permutation 27, Normalised statistic = 0.9977589730413136
Compressor Thread-1 Permutation 28, Normalised statistic = 0.9980023039867137
Compressor Thread-2 Permutation 28, Normalised statistic = 0.9984549335774584
Compressor Thread-3 Permutation 28, Normalised statistic = 0.9999387418598993
Compressor Thread-0 Permutation 28, Normalised statistic = 0.9976534729111399
Compressor Thread-4 Permutation 28, Normalised statistic = 0.9989926439183429
CURRENT RANK = 110
Remaining running time to full completion = 6353s
Estimated full completion date/time = 2020-12-17T22:41:26.671464
----------------------------------
Ranked as > 110/10,000
*** PASSED permutation test. There is no evidence that the data is not IID ***
Based on 140 permutations.
Test results in file: /tmp/results.json
----------------------------------
Compressor Thread-1 Permutation 29, Normalised statistic = 0.9974645936458293
Compressor Thread-0 Permutation 29, Normalised statistic = 1.0009512027865648
Compressor Thread-3 Permutation 29, Normalised statistic = 0.9989943455333457
Compressor Thread-4 Permutation 29, Normalised statistic = 0.9996545721544318
Compressor Thread-2 Permutation 29, Normalised statistic = 0.9969915446750511