Using BSI AIS 20/31
Bundesamt für Sicherheit in der Informationstechnik (BSI) AIS 20/31 is another (European) standard for raw entropy measurement. Here TRNG designers are required to provide a stochastic model of the entropy source, so the entropy can be estimated in theory according to the model. The risk is that the model is unrepresentative of the sample data set, yet there is no hard requirement to assess the goodness of fit. It state that it should be checked to see if it fits, whilst at the same time being as simple as possible. Indeed the standard explicitly says:-
In particular, precise physical models of ‘real-world’ physical RNGs (typically based on electronic circuits) usually cannot easily be formulated and are not analyzed.
We are not sure how we can comply for quantum entropy sources such as Zener diodes and photo-sensors, never mind JPEG encoding of them. The standard (§ 2.4.1) does not shy away from early compression of the raw entropy signal to assist in eliminating simple correlations. Significant correlations remain problematic resulting in non-IID data. This is another example of manipulation of the raw entropy prior to measurement that is commonly implied by standards[1][2]. And in a parallel to 90B, gross errors will result if performed on data that significantly diverges from uniform, such as normal or log-normal distributions which are typical of Zener avalanche effect sampling.
Analogue to digital converters (ADCs) and associated amplifiers are hugely influenced by slew rates and capacitance. There is even a capacitor specifically for holding the sample steady in an ADC. Photo-sensors affect adjacent photo-sensors in CMOS arrays. Junction capacitance affects Zener diodes. Consequently, most real world entropy samples are correlated. JPEG files are more correlated than most sensors. With this in mind, we will not aim for stochastic modelling of our entropy sources, but rely on direct empirical measurement of distributions such as:-
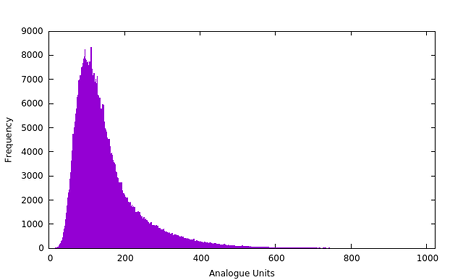
Raw sample distribution from a single Zener diode.
We could take the risky approach and generate conservative models that grossly overestimate our entropy rates, ignore autocorrelation and then compensate downwards. A quantized log-normal distribution would seem a candidate fit to the above. In that case though, why not just measure via compression and divide by a safety factor?
And the state of the art compressors (cmix, paq8 etc.) are surprisingly accurate at entropy measurement. Testing against synthetic data sets suggests accuracy of 0.1% compared to the theoretical Shannon entropies. Accuracy drops for more complex correlated data such as the classic enwik8/9 test files from the Hutter Prize competition. Fortunately, natural sample data is not as complex nor as correlated as language and Wikipedia entries. The above log-normal example only features an autocorrelation lag of $ n = 3 $. Therefore entropy measurement via strong compression is valid and accurate to within the theoretical 0.1% figure. Large correlation lag is unlikely to exceed $ n = 100$ in the majority of cases. If measurement accuracy is defined as $ \frac{H_{theoretical}}{H_{compress}} $, then we find the following normalised relationship for smallish $n$:-
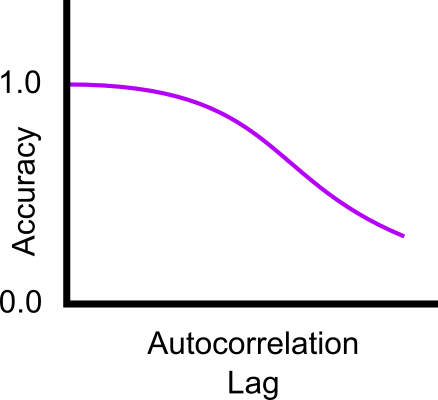
Normalised theoretical to compressive entropy measurement accuracy.
The curve ultimately becomes asymptotic to some unknown error rate at the Kolmogorov (algorithmic) complexity of the sample data as $ n \rightarrow \infty $. You can choose to believe in the Hilberg Conjecture[3] if you want to, but it seems like mathematical hubris to attempt to reduce Shakespeare’s life work to just $ Bn^{\beta} $.
References:-
[1] John Kelsey, Kerry A. McKay and Meltem Sönmez Turan, Predictive Models for Min-Entropy Estimation.
[2] Joseph D. Hart, Yuta Terashima, Atsushi Uchida, Gerald B. Baumgartner, Thomas E. Murphy and Rajarshi Roy, Recommendations and illustrations for the evaluation of photonic random number generators.
[3] Hilberg W., Der bekannte Grenzwert der redundanzfreien Information in Texten – eine Fehlinterpretation der Shannonschen Experimente? Frequenz 44, 1990, pp. 243–248.