Accurate entropy measurement
Measurement
We can (in a way) cheat here. A common model for a generic entropy source (repurposed for the Photonic Instrument) is:-
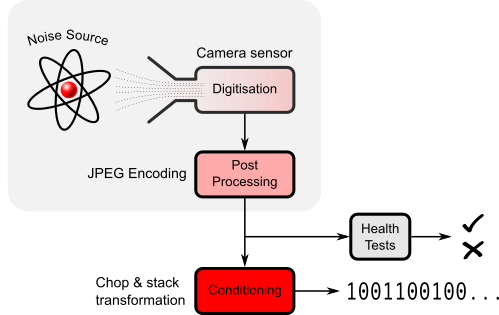
Photonic Instrument wrt generic model of an entropy source.
A degree of conditioning of the raw data is allowable as long as the total entropy rate of the source is not increased. No deterministic technique can. But we can reduce it by our magical chop & stack transformation. The conditioning transforms a non deterministic normally distributed as $\mathcal{N}(\mu, \sigma^2)$ length JPEG file to a fixed length. The technique is outlined below:-
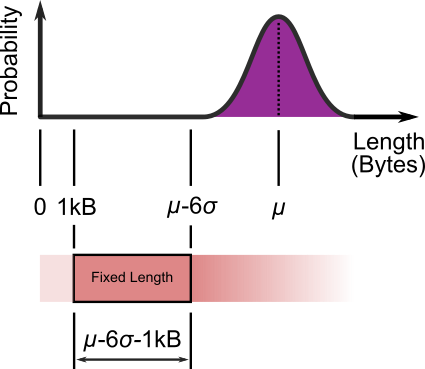
Head & tailing original JPEG file of length $\mathcal{N}(\mu, \sigma^2)$.
Start by chopping off the first 1,000 bytes; Header information lives there. Then chop off everything after $\mu - 6 \sigma$ bytes. A segment $\mu - 6 \sigma - 1,000$ bytes long will be left. Thus of fixed length. This length may have to be slightly tweaked to allow folding(re-shaping) of the block on divisible by four byte boundaries. The Six Sigma value is a somewhat arbitrary management fad, but it covers 99.999 999 802 7% of our JPEG sizes and still allows for long term sensor drift. Then fold and stack the fixed length segment as:-
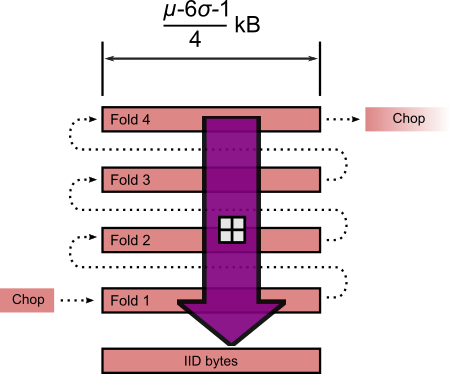
Folding standardised length JPEG segment and modular addition.
Once the folds are summed modulo 256, we should have an IID block of fixed length $ \frac{\mu - 6 \sigma - 1,000 - t}{4} $ bytes, where $t$ is the tweak (-2 bytes in this case). Which is implemented in Python 3 thusly:-
"""
Chop & stack JPEG method to create IID data.
Mean file/jpeg size = 19.46 kB
Std. dev. = 0.161 kB
Works very well with 4 folds.
So outputs will be 4,373 B each.
"""
import matplotlib.pyplot as plt
import numpy
import requests
url = 'http://192.168.***.***/snapshot.cgi?user=******&pwd=*************'
no_frames = 1_000
head_chop = 1_000
tail_chop = 19_460 - (6 * 161) - 2 # (-2) tweak needed so that can fold exactly 4.0 times.
with open('/tmp/r', 'wb') as f:
for i in range(no_frames):
print(i)
response = requests.get(url).content
a = numpy.fromiter(response, numpy.uint8)
b = a[head_chop:tail_chop] # Head & tail.
c = numpy.reshape(b, (4, -1)) # Stack folds.
d = c.sum(axis=0) % 256 # Modular addition.
f.write(d.astype(numpy.uint8))
# Graph last frame to visually check.
plt.plot(d, color='purple')
plt.xlabel('Position')
plt.ylabel('Value')
plt.show()The following waveform and histogram demonstrates the quality of our conditioning. Compare it with a histogram of a raw JPEG from the Photonic Instrument here. But we will test the IID hypothesis rigorously for JPEG files of $\mathcal{N}(19460, 161^2)$ bytes…
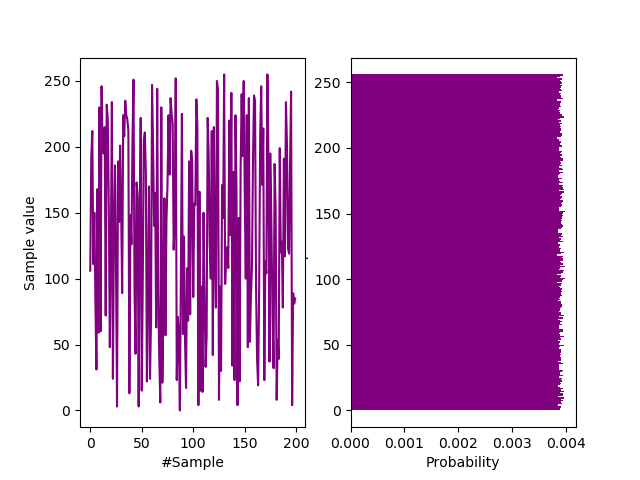
Sample and histogram of transformation output.
From the above probability mass function, we can immediately visually estimate $ H_{\infty} \approx -\log_2(0.004) = 7.97$ bits/byte. Let’s check for IIDdness:-
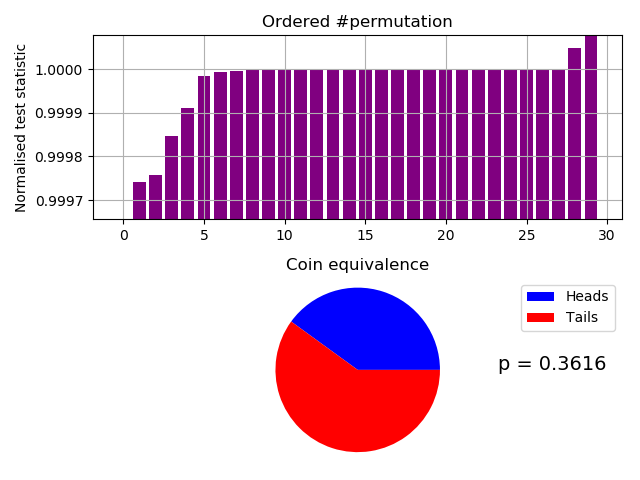
Our fast IID test of transformation output.
Starting IID test...
Baseline: 16073743
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Compressor Thread-0 started.
Compressor Thread-4 started.
Compressor Thread-3 started.
Compressor Thread-1 started.
Compressor Thread-2 started.
Compressor Thread-3 Permutation 1Compressor Thread-4 Permutation 1Compressor Thread-2 Permutation 1, Normalised statistic = 0.999977043305968
, Normalised statistic = 1.000015180036162
, Normalised statistic = 0.99998002954259
Compressor Thread-1 Permutation 1, Normalised statistic = 0.9999926588349708
Compressor Thread-0 Permutation 1, Normalised statistic = 0.9999565751424544
Compressor Thread-4 Permutation 2, Normalised statistic = 1.0000358348394647
Compressor Thread-2 Permutation 2, Normalised statistic = 1.0000304844988501
Compressor Thread-0 Permutation 2, Normalised statistic = 1.000041185180079
Compressor Thread-1 Permutation 2, Normalised statistic = 0.9999896725983487
Compressor Thread-3 Permutation 2, Normalised statistic = 1.0000296135131685
Compressor Thread-2 Permutation 3, Normalised statistic = 0.9999507893089992
Compressor Thread-3 Permutation 3, Normalised statistic = 0.9999975114694817
Compressor Thread-4 Permutation 3, Normalised statistic = 1.0000111361740698
Compressor Thread-0 Permutation 3, Normalised statistic = 0.9999780387181754
Compressor Thread-1 Permutation 3, Normalised statistic = 1.000074966981866
CURRENT RANK = 8
Remaining running time to full completion = 6672s
Estimated full completion date/time = 2021-05-10T14:49:08.928771
Compressor Thread-4 Permutation 4, Normalised statistic = 0.9999775410120717
Compressor Thread-2 Permutation 4, Normalised statistic = 1.0000110117475438
Compressor Thread-3 Permutation 4, Normalised statistic = 1.0000357104129387
Compressor Thread-1 Permutation 4, Normalised statistic = 1.0000172952871027
Compressor Thread-0 Permutation 4, Normalised statistic = 0.9999660315584242
Compressor Thread-3 Permutation 5, Normalised statistic = 0.9999827047128973
Compressor Thread-4 Permutation 5, Normalised statistic = 0.999970821979672
Compressor Thread-2 Permutation 5, Normalised statistic = 0.9999757990407088
Compressor Thread-1 Permutation 5, Normalised statistic = 0.9999996267204222
Compressor Thread-0 Permutation 5, Normalised statistic = 0.9999607434310727
Compressor Thread-3 Permutation 6, Normalised statistic = 0.9999603701514949
Compressor Thread-4 Permutation 6, Normalised statistic = 1.0000105762547031
Compressor Thread-0 Permutation 6, Normalised statistic = 0.9999976358960075
Compressor Thread-2 Permutation 6, Normalised statistic = 0.9999789097038568
Compressor Thread-1 Permutation 6, Normalised statistic = 0.9999799051160642
CURRENT RANK = 19
Remaining running time to full completion = 6662s
Estimated full completion date/time = 2021-05-10T14:49:08.928771
Compressor Thread-3 Permutation 7, Normalised statistic = 1.000018166272784
Compressor Thread-4 Permutation 7, Normalised statistic = 0.9999812115945863
Compressor Thread-0 Permutation 7, Normalised statistic = 1.0000064079660849
Compressor Thread-2 Permutation 7, Normalised statistic = 0.9999935298206523
Compressor Thread-1 Permutation 7, Normalised statistic = 1.000018166272784
Compressor Thread-3 Permutation 8, Normalised statistic = 1.000018539552362
Compressor Thread-4 Permutation 8, Normalised statistic = 0.9999700132072535
Compressor Thread-0 Permutation 8, Normalised statistic = 0.9999753013346051
Compressor Thread-2 Permutation 8, Normalised statistic = 1.0000086476435512
Compressor Thread-1 Permutation 8, Normalised statistic = 0.9999849443903638
Compressor Thread-3 Permutation 9, Normalised statistic = 0.999999875573474
Compressor Thread-4 Permutation 9, Normalised statistic = 0.9999948362991744
Compressor Thread-2 Permutation 9, Normalised statistic = 0.9999955206450669
Compressor Thread-0 Permutation 9, Normalised statistic = 1.0000095808424958
Compressor Thread-1 Permutation 9, Normalised statistic = 0.9999976358960075
Compressor Thread-3 Permutation 10, Normalised statistic = 0.9999948362991744
Compressor Thread-4 Permutation 10, Normalised statistic = 0.9999657827053724
Compressor Thread-2 Permutation 10, Normalised statistic = 1.000003110663148
Compressor Thread-0 Permutation 10, Normalised statistic = 1.0000294890866428
Compressor Thread-1 Permutation 10, Normalised statistic = 0.9999670269706316
CURRENT RANK = 31
Remaining running time to full completion = 5984s
Estimated full completion date/time = 2021-05-10T14:38:00.928771
Compressor Thread-3 Permutation 11, Normalised statistic = 0.9999643518003243
Compressor Thread-4 Permutation 11, Normalised statistic = 1.0000095186292328
Compressor Thread-0 Permutation 11, Normalised statistic = 0.9999951473654892
Compressor Thread-2 Permutation 11, Normalised statistic = 0.9999537133323583
Compressor Thread-1 Permutation 11, Normalised statistic = 1.0000033595162
Compressor Thread-3 Permutation 12, Normalised statistic = 0.9999883661198266
Compressor Thread-4 Permutation 12, Normalised statistic = 1.0000431760044939
Compressor Thread-0 Permutation 12, Normalised statistic = 1.0000078388711329
Compressor Thread-1 Permutation 12, Normalised statistic = 0.999966342624739
Compressor Thread-2 Permutation 12, Normalised statistic = 0.9999528423466768
Compressor Thread-3 Permutation 13, Normalised statistic = 0.9999833890587898
Compressor Thread-4 Permutation 13, Normalised statistic = 1.0000021774642036
Compressor Thread-1 Permutation 13, Normalised statistic = 1.0000242631725542
Compressor Thread-2 Permutation 13, Normalised statistic = 1.0000068434589255
Compressor Thread-0 Permutation 13, Normalised statistic = 0.9999468698734327
CURRENT RANK = 39
Remaining running time to full completion = 6128s
Estimated full completion date/time = 2021-05-10T14:40:34.928771
Compressor Thread-3 Permutation 14, Normalised statistic = 0.9999900458779265
Compressor Thread-4 Permutation 14, Normalised statistic = 1.0000077766578699
Compressor Thread-1 Permutation 14, Normalised statistic = 1.0000257562908652
Compressor Thread-2 Permutation 14, Normalised statistic = 0.9999902947309783
Compressor Thread-0 Permutation 14, Normalised statistic = 0.9999621121228578
Compressor Thread-3 Permutation 15, Normalised statistic = 0.999984695537312
Compressor Thread-4 Permutation 15, Normalised statistic = 1.000015117822899
Compressor Thread-1 Permutation 15, Normalised statistic = 0.9999904191575043
Compressor Thread-2 Permutation 15, Normalised statistic = 0.9999875573474082
Compressor Thread-0 Permutation 15, Normalised statistic = 1.0000020530376776
Compressor Thread-3 Permutation 16, Normalised statistic = 1.0000027373835703
Compressor Thread-4 Permutation 16, Normalised statistic = 0.9999718796051423
Compressor Thread-1 Permutation 16, Normalised statistic = 0.999924970804871
Compressor Thread-2 Permutation 16, Normalised statistic = 0.9999689555817833
Compressor Thread-0 Permutation 16, Normalised statistic = 0.9999996889336852
Compressor Thread-3 Permutation 17, Normalised statistic = 1.0000410607535533
Compressor Thread-4 Permutation 17, Normalised statistic = 1.0000316665508464
Compressor Thread-1 Permutation 17, Normalised statistic = 0.9999906680105561
Compressor Thread-0 Permutation 17, Normalised statistic = 1.0000253207980245
Compressor Thread-2 Permutation 17, Normalised statistic = 1.0000094564159698
CURRENT RANK = 50
Remaining running time to full completion = 5846s
Estimated full completion date/time = 2021-05-10T14:36:02.928771
Compressor Thread-3 Permutation 18, Normalised statistic = 1.0000072789517662
Compressor Thread-4 Permutation 18, Normalised statistic = 0.9999840111914194
Compressor Thread-1 Permutation 18, Normalised statistic = 0.999978536424279
Compressor Thread-2 Permutation 18, Normalised statistic = 1.0000177307799434
Compressor Thread-0 Permutation 18, Normalised statistic = 0.9999968271235891
Compressor Thread-3 Permutation 19, Normalised statistic = 1.0000433626442826
Compressor Thread-4 Permutation 19, Normalised statistic = 0.9999805272486937
Compressor Thread-1 Permutation 19, Normalised statistic = 0.9999593747392875
Compressor Thread-2 Permutation 19, Normalised statistic = 0.9999961427776966
Compressor Thread-0 Permutation 19, Normalised statistic = 1.0000253207980245
Compressor Thread-3 Permutation 20, Normalised statistic = 0.9999857531627823
Compressor Thread-4 Permutation 20, Normalised statistic = 0.9999767322396532
Compressor Thread-1 Permutation 20, Normalised statistic = 1.000019908244147
Compressor Thread-2 Permutation 20, Normalised statistic = 0.9999903569442413
Compressor Thread-0 Permutation 20, Normalised statistic = 0.9999566995689803
Compressor Thread-3 Permutation 21, Normalised statistic = 0.9999695777144129
Compressor Thread-4 Permutation 21, Normalised statistic = 1.000006283539559
Compressor Thread-1 Permutation 21, Normalised statistic = 0.9999868730015156
Compressor Thread-2 Permutation 21, Normalised statistic = 0.9999792829834345
Compressor Thread-0 Permutation 21, Normalised statistic = 0.9999318142637965
CURRENT RANK = 64
Remaining running time to full completion = 5667s
Estimated full completion date/time = 2021-05-10T14:33:13.928771
Compressor Thread-3 Permutation 22, Normalised statistic = 0.9999697021409388
Compressor Thread-4 Permutation 22, Normalised statistic = 1.0000174197136287
Compressor Thread-1 Permutation 22, Normalised statistic = 0.9999868730015156
Compressor Thread-2 Permutation 22, Normalised statistic = 0.999950975948788
Compressor Thread-0 Permutation 22, Normalised statistic = 1.0000663193383146
Compressor Thread-3 Permutation 23, Normalised statistic = 0.9999854420964676
Compressor Thread-4 Permutation 23, Normalised statistic = 0.9999692044348352
Compressor Thread-2 Permutation 23, Normalised statistic = 0.9999766700263902
Compressor Thread-1 Permutation 23, Normalised statistic = 0.9999649117196909
Compressor Thread-0 Permutation 23, Normalised statistic = 1.0000205925900396
Compressor Thread-3 Permutation 24, Normalised statistic = 0.9999860642290971
Compressor Thread-4 Permutation 24, Normalised statistic = 0.9999762345335496
Compressor Thread-2 Permutation 24, Normalised statistic = 0.9999792207701715
Compressor Thread-0 Permutation 24, Normalised statistic = 0.9999715685388276
Compressor Thread-1 Permutation 24, Normalised statistic = 1.0000281826081205
Compressor Thread-3 Permutation 25, Normalised statistic = 1.0000132514250104
CURRENT RANK = 75
Remaining running time to full completion = 5728s
Estimated full completion date/time = 2021-05-10T14:34:24.928771
Compressor Thread-4 Permutation 25, Normalised statistic = 0.9999874951341452
Compressor Thread-2 Permutation 25, Normalised statistic = 1.0000617777701186
Compressor Thread-0 Permutation 25, Normalised statistic = 1.0000545610316154
Compressor Thread-1 Permutation 25, Normalised statistic = 0.999947989712166
Compressor Thread-3 Permutation 26, Normalised statistic = 0.9999704487000943
Compressor Thread-4 Permutation 26, Normalised statistic = 0.999998444668426
Compressor Thread-2 Permutation 26, Normalised statistic = 0.9999978225357964
Compressor Thread-0 Permutation 26, Normalised statistic = 0.9999490473376363
Compressor Thread-1 Permutation 26, Normalised statistic = 0.9999822692200566
Compressor Thread-3 Permutation 27, Normalised statistic = 0.9999343027943149
Compressor Thread-4 Permutation 27, Normalised statistic = 0.9999675246767352
Compressor Thread-2 Permutation 27, Normalised statistic = 0.999972377311246
Compressor Thread-0 Permutation 27, Normalised statistic = 1.0000547476714041
Compressor Thread-1 Permutation 27, Normalised statistic = 0.9999748658417644
Compressor Thread-3 Permutation 28, Normalised statistic = 1.0000133136382734
Compressor Thread-4 Permutation 28, Normalised statistic = 0.9999580060475024
Compressor Thread-2 Permutation 28, Normalised statistic = 1.000022956694032
Compressor Thread-0 Permutation 28, Normalised statistic = 0.9999906057972932
Compressor Thread-1 Permutation 28, Normalised statistic = 1.0000068434589255
CURRENT RANK = 88
Remaining running time to full completion = 5647s
Estimated full completion date/time = 2021-05-10T14:33:13.928771
Compressor Thread-3 Permutation 29, Normalised statistic = 1.0000112606005958
Compressor Thread-4 Permutation 29, Normalised statistic = 1.0000481530655305
Compressor Thread-2 Permutation 29, Normalised statistic = 0.9999959561379076
Compressor Thread-0 Permutation 29, Normalised statistic = 0.9999899836646635
Compressor Thread-1 Permutation 29, Normalised statistic = 1.000036456972094
Compressor Thread-3 Permutation 30, Normalised statistic = 0.9999913523564486
Compressor Thread-4 Permutation 30, Normalised statistic = 1.000001493118311
Compressor Thread-2 Permutation 30, Normalised statistic = 0.999967773529787
Compressor Thread-1 Permutation 30, Normalised statistic = 0.9999942141665448
Compressor Thread-0 Permutation 30, Normalised statistic = 1.000032102043687
Compressor Thread-3 Permutation 31, Normalised statistic = 1.000084174544784
Compressor Thread-4 Permutation 31, Normalised statistic = 0.9999825802863714
Compressor Thread-2 Permutation 31, Normalised statistic = 1.000033657375261
Compressor Thread-1 Permutation 31, Normalised statistic = 1.0000156777422657
Compressor Thread-0 Permutation 31, Normalised statistic = 0.999981771513953
Compressor Thread-3 Permutation 32, Normalised statistic = 1.0000070923119773
Compressor Thread-4 Permutation 32, Normalised statistic = 1.000010700681229
Compressor Thread-2 Permutation 32, Normalised statistic = 1.000006034686507
Compressor Thread-1 Permutation 32, Normalised statistic = 1.0000102029751254
Compressor Thread-0 Permutation 32, Normalised statistic = 1.0000149933963731
CURRENT RANK = 95
Remaining running time to full completion = 5548s
Estimated full completion date/time = 2021-05-10T14:31:44.928771
Compressor Thread-3 Permutation 33, Normalised statistic = 0.999989361532034
Compressor Thread-4 Permutation 33, Normalised statistic = 0.9999867485749897
Compressor Thread-2 Permutation 33, Normalised statistic = 1.0000202193104617
Compressor Thread-1 Permutation 33, Normalised statistic = 0.9999598724453912
Compressor Thread-0 Permutation 33, Normalised statistic = 0.999961801056543
Compressor Thread-3 Permutation 34, Normalised statistic = 0.9999833268455269
Compressor Thread-4 Permutation 34, Normalised statistic = 0.9999911035033968
Compressor Thread-2 Permutation 34, Normalised statistic = 0.9999940897400189
Compressor Thread-1 Permutation 34, Normalised statistic = 0.9999845088975231
Compressor Thread-0 Permutation 34, Normalised statistic = 0.9999824558598455
Compressor Thread-3 Permutation 35, Normalised statistic = 1.0000344039344164
Compressor Thread-4 Permutation 35, Normalised statistic = 0.9999875573474082
Compressor Thread-2 Permutation 35, Normalised statistic = 0.9999872462810934
Compressor Thread-1 Permutation 35, Normalised statistic = 0.999992472195182
Compressor Thread-0 Permutation 35, Normalised statistic = 0.9999641651605354
Compressor Thread-3 Permutation 36, Normalised statistic = 1.0000441092034382
CURRENT RANK = 108
Remaining running time to full completion = 5595s
Estimated full completion date/time = 2021-05-10T14:32:41.928771
----------------------------------
Ranked as > 108/10,000
*** PASSED permutation test. There is no evidence that the data is not IID ***
Based on 176 permutations.
Test results in file: /tmp/results.json
----------------------------------
Compressor Thread-4 Permutation 36, Normalised statistic = 0.9999894859585599
Compressor Thread-2 Permutation 36, Normalised statistic = 0.9999749280550274
Compressor Thread-0 Permutation 36, Normalised statistic = 1.0000133758515362
Compressor Thread-1 Permutation 36, Normalised statistic = 0.9999851310301527
Compressor Thread-3 Permutation 37, Normalised statistic = 0.9999766078131272
Our slow IID test of transformation output.
ea_iid /tmp/r
Calculating baseline statistics...
H_original: 7.940423
H_bitstring: 0.999237
min(H_original, 8 X H_bitstring): 7.940423 <======= Min. Entropy.
** Passed chi square tests
** Passed length of longest repeated substring test
Beginning initial tests...
Beginning permutation tests... these may take some time
** Passed IID permutation testsOur fast, slow and the NIST 800-90B IID tests all confirm that the JPEG segments are indeed IID. Whoopie! So we get min(H_original, 8 X H_bitstring): 7.940423 bits/byte. Let’s just say $H_{\infty} = 7.9$ bits/byte for 4,373 byte long transformed JPEG segments. That’s a min.entropy of 34.5 kbits per segment/frame.
This 4 MB test file r, made from 1,000 conditioned Photonic JPEG frames is available under Related Files at the bottom of the page.
But there’s more! Our chop & stack technique is so good that the IID output file passes cryptographic randomness test suite Special Publication (NIST SP) - 800-22 Rev 1a as detailed below:-
------------------------------------------------------------------------------
RESULTS FOR THE UNIFORMITY OF P-VALUES AND THE PROPORTION OF PASSING SEQUENCES
------------------------------------------------------------------------------
generator is </tmp/r>
------------------------------------------------------------------------------
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 P-VALUE PROPORTION STATISTICAL TEST
------------------------------------------------------------------------------
0 4 0 1 0 1 1 1 2 0 0.122325 10/10 Frequency
2 1 0 1 0 2 1 1 1 1 0.911413 10/10 BlockFrequency
1 1 0 2 1 2 1 0 2 0 0.739918 10/10 CumulativeSums
0 1 3 0 1 0 2 0 1 2 0.350485 10/10 CumulativeSums
1 2 1 2 0 0 2 1 1 0 0.739918 10/10 Runs
0 1 1 1 0 1 2 0 1 3 0.534146 10/10 LongestRun
0 1 0 2 0 0 2 3 2 0 0.213309 10/10 Rank
1 1 1 0 2 0 3 2 0 0 0.350485 10/10 FFT
0 1 2 2 0 0 2 0 1 2 0.534146 10/10 NonOverlappingTemplate
0 2 0 1 0 4 0 1 1 1 0.122325 10/10 NonOverlappingTemplate
0 2 0 2 0 0 1 3 1 1 0.350485 10/10 NonOverlappingTemplate
0 0 1 1 0 3 1 1 2 1 0.534146 10/10 NonOverlappingTemplate
0 3 0 2 2 2 0 0 0 1 0.213309 10/10 NonOverlappingTemplate
0 2 1 0 1 1 2 2 1 0 0.739918 10/10 NonOverlappingTemplate
1 1 0 0 1 4 0 2 0 1 0.122325 10/10 NonOverlappingTemplate
1 1 1 1 1 1 1 0 1 2 0.991468 10/10 NonOverlappingTemplate
0 2 1 1 2 0 0 0 3 1 0.350485 10/10 NonOverlappingTemplate
3 2 0 0 0 1 2 1 0 1 0.350485 10/10 NonOverlappingTemplate
0 3 0 0 2 1 1 2 0 1 0.350485 10/10 NonOverlappingTemplate
1 2 1 0 3 0 1 0 0 2 0.350485 10/10 NonOverlappingTemplate
1 4 1 0 1 1 0 1 0 1 0.213309 10/10 NonOverlappingTemplate
1 0 1 3 0 2 0 1 0 2 0.350485 10/10 NonOverlappingTemplate
0 1 1 0 0 1 1 1 2 3 0.534146 10/10 NonOverlappingTemplate
0 3 2 0 1 0 1 1 0 2 0.350485 10/10 NonOverlappingTemplate
1 1 4 0 0 1 0 1 1 1 0.213309 10/10 NonOverlappingTemplate
0 1 2 0 2 0 1 3 0 1 0.350485 10/10 NonOverlappingTemplate
2 1 1 0 2 0 0 0 2 2 0.534146 9/10 NonOverlappingTemplate
1 0 1 0 2 1 1 1 2 1 0.911413 10/10 NonOverlappingTemplate
1 2 0 1 0 0 0 2 1 3 0.350485 10/10 NonOverlappingTemplate
1 1 0 1 0 2 0 3 2 0 0.350485 10/10 NonOverlappingTemplate
1 1 2 1 1 1 2 1 0 0 0.911413 10/10 NonOverlappingTemplate
3 1 3 0 0 0 2 0 0 1 0.122325 10/10 NonOverlappingTemplate
1 0 1 1 0 0 3 1 1 2 0.534146 10/10 NonOverlappingTemplate
0 1 2 2 1 0 1 2 0 1 0.739918 10/10 NonOverlappingTemplate
2 0 2 1 1 1 0 0 3 0 0.350485 10/10 NonOverlappingTemplate
0 0 0 1 1 2 0 2 3 1 0.350485 10/10 NonOverlappingTemplate
1 0 2 1 1 2 2 0 0 1 0.739918 10/10 NonOverlappingTemplate
1 1 0 1 0 0 3 1 1 2 0.534146 10/10 NonOverlappingTemplate
1 0 1 1 0 0 2 1 1 3 0.534146 10/10 NonOverlappingTemplate
0 4 0 1 2 0 1 1 0 1 0.122325 10/10 NonOverlappingTemplate
2 0 1 3 1 0 1 0 0 2 0.350485 10/10 NonOverlappingTemplate
0 0 2 0 1 2 1 2 0 2 0.534146 10/10 NonOverlappingTemplate
2 0 2 3 1 1 0 0 1 0 0.350485 9/10 NonOverlappingTemplate
1 1 2 1 1 0 1 0 2 1 0.911413 10/10 NonOverlappingTemplate
0 1 1 2 2 0 0 0 1 3 0.350485 10/10 NonOverlappingTemplate
1 1 1 1 1 1 2 1 1 0 0.991468 10/10 NonOverlappingTemplate
0 0 2 2 1 1 1 0 2 1 0.739918 10/10 NonOverlappingTemplate
0 3 2 1 1 0 1 0 0 2 0.350485 10/10 NonOverlappingTemplate
1 0 1 0 2 2 1 2 0 1 0.739918 10/10 NonOverlappingTemplate
0 1 1 0 1 1 2 1 1 2 0.911413 10/10 NonOverlappingTemplate
2 2 1 0 2 0 0 2 0 1 0.534146 10/10 NonOverlappingTemplate
0 1 0 0 2 2 4 0 1 0 0.066882 10/10 NonOverlappingTemplate
0 3 0 1 1 0 1 3 1 0 0.213309 10/10 NonOverlappingTemplate
0 1 1 1 0 0 3 1 2 1 0.534146 10/10 NonOverlappingTemplate
0 1 2 0 2 1 1 2 0 1 0.739918 10/10 NonOverlappingTemplate
2 1 0 3 2 1 1 0 0 0 0.350485 10/10 NonOverlappingTemplate
2 0 0 0 0 0 1 3 3 1 0.122325 10/10 NonOverlappingTemplate
2 1 1 1 1 2 0 1 1 0 0.911413 10/10 NonOverlappingTemplate
1 1 1 1 1 0 2 1 2 0 0.911413 10/10 NonOverlappingTemplate
0 1 0 1 1 2 3 1 0 1 0.534146 10/10 NonOverlappingTemplate
1 2 0 0 0 3 3 0 0 1 0.122325 10/10 NonOverlappingTemplate
1 1 1 0 0 4 1 0 0 2 0.122325 10/10 NonOverlappingTemplate
0 2 2 1 1 0 1 1 1 1 0.911413 10/10 NonOverlappingTemplate
2 1 1 1 1 1 2 0 1 0 0.911413 9/10 NonOverlappingTemplate
2 0 3 0 1 1 1 1 1 0 0.534146 10/10 NonOverlappingTemplate
0 1 2 2 1 1 1 0 2 0 0.739918 10/10 NonOverlappingTemplate
2 1 1 2 0 2 0 1 0 1 0.739918 10/10 NonOverlappingTemplate
1 0 2 3 0 0 1 1 2 0 0.350485 10/10 NonOverlappingTemplate
1 0 1 1 3 1 0 3 0 0 0.213309 10/10 NonOverlappingTemplate
1 0 2 0 1 0 1 1 1 3 0.534146 10/10 NonOverlappingTemplate
2 1 1 1 0 0 0 2 2 1 0.739918 10/10 NonOverlappingTemplate
0 1 0 0 2 0 2 0 2 3 0.213309 10/10 NonOverlappingTemplate
1 2 0 3 0 1 0 1 1 1 0.534146 10/10 NonOverlappingTemplate
0 1 2 1 1 1 0 1 3 0 0.534146 10/10 NonOverlappingTemplate
1 1 1 0 1 0 2 1 2 1 0.911413 10/10 NonOverlappingTemplate
1 2 1 1 1 0 1 1 0 2 0.911413 10/10 NonOverlappingTemplate
1 2 0 1 2 1 1 1 1 0 0.911413 10/10 NonOverlappingTemplate
1 0 3 0 1 1 1 2 1 0 0.534146 10/10 NonOverlappingTemplate
1 0 2 1 1 2 0 3 0 0 0.350485 10/10 NonOverlappingTemplate
0 0 3 3 2 0 1 0 1 0 0.122325 10/10 NonOverlappingTemplate
2 1 1 1 1 2 0 1 1 0 0.911413 10/10 NonOverlappingTemplate
1 2 0 0 4 1 0 1 0 1 0.122325 10/10 NonOverlappingTemplate
0 1 2 2 0 0 2 0 1 2 0.534146 10/10 NonOverlappingTemplate
1 2 1 0 1 0 2 0 1 2 0.739918 10/10 NonOverlappingTemplate
1 1 0 0 2 0 1 2 1 2 0.739918 10/10 NonOverlappingTemplate
3 2 1 0 0 1 0 0 1 2 0.350485 10/10 NonOverlappingTemplate
0 3 0 1 1 1 2 1 0 1 0.534146 10/10 NonOverlappingTemplate
0 2 1 2 0 0 1 3 0 1 0.350485 10/10 NonOverlappingTemplate
2 0 1 1 0 1 0 2 1 2 0.739918 10/10 NonOverlappingTemplate
2 0 2 0 0 3 0 2 1 0 0.213309 10/10 NonOverlappingTemplate
1 0 1 1 3 1 1 1 0 1 0.739918 10/10 NonOverlappingTemplate
0 1 1 2 0 2 0 1 3 0 0.350485 10/10 NonOverlappingTemplate
0 2 0 3 1 2 0 0 1 1 0.350485 10/10 NonOverlappingTemplate
4 0 0 1 0 1 0 1 1 2 0.122325 10/10 NonOverlappingTemplate
4 1 0 1 0 1 2 0 0 1 0.122325 10/10 NonOverlappingTemplate
2 0 0 1 0 0 1 2 4 0 0.066882 9/10 NonOverlappingTemplate
1 1 2 1 0 0 2 2 1 0 0.739918 10/10 NonOverlappingTemplate
1 0 0 1 0 3 1 1 1 2 0.534146 10/10 NonOverlappingTemplate
1 2 2 0 2 1 0 0 0 2 0.534146 10/10 NonOverlappingTemplate
1 0 2 0 2 1 1 0 1 2 0.739918 10/10 NonOverlappingTemplate
1 0 2 1 0 3 0 2 1 0 0.350485 10/10 NonOverlappingTemplate
3 2 1 0 0 0 2 0 2 0 0.213309 10/10 NonOverlappingTemplate
1 1 0 1 2 0 2 1 1 1 0.911413 10/10 NonOverlappingTemplate
2 0 1 0 1 1 1 0 2 2 0.739918 10/10 NonOverlappingTemplate
0 0 1 1 2 3 1 1 1 0 0.534146 10/10 NonOverlappingTemplate
1 4 1 0 0 0 2 1 0 1 0.122325 10/10 NonOverlappingTemplate
0 2 1 1 1 2 3 0 0 0 0.350485 10/10 NonOverlappingTemplate
0 0 2 1 2 2 0 0 1 2 0.534146 10/10 NonOverlappingTemplate
2 1 1 1 2 1 0 0 1 1 0.911413 9/10 NonOverlappingTemplate
0 0 0 1 1 1 1 4 2 0 0.122325 10/10 NonOverlappingTemplate
1 1 1 2 0 0 2 0 1 2 0.739918 9/10 NonOverlappingTemplate
0 2 0 2 0 2 1 1 1 1 0.739918 10/10 NonOverlappingTemplate
0 1 1 0 0 2 0 2 1 3 0.350485 10/10 NonOverlappingTemplate
0 1 1 0 3 0 0 1 2 2 0.350485 10/10 NonOverlappingTemplate
1 2 1 0 2 0 1 1 1 1 0.911413 10/10 NonOverlappingTemplate
0 4 1 0 2 0 1 1 0 1 0.122325 10/10 NonOverlappingTemplate
2 1 0 1 0 0 1 2 1 2 0.739918 10/10 NonOverlappingTemplate
1 2 0 1 0 0 2 2 1 1 0.739918 10/10 NonOverlappingTemplate
0 2 2 1 2 0 1 0 0 2 0.534146 10/10 NonOverlappingTemplate
0 1 2 0 0 2 1 2 0 2 0.534146 10/10 NonOverlappingTemplate
0 0 0 4 1 1 0 1 0 3 0.035174 10/10 NonOverlappingTemplate
0 1 1 1 1 2 0 1 1 2 0.911413 10/10 NonOverlappingTemplate
0 0 3 1 0 0 1 3 2 0 0.122325 10/10 NonOverlappingTemplate
0 0 0 1 1 2 1 3 1 1 0.534146 10/10 NonOverlappingTemplate
2 1 2 2 0 1 0 1 0 1 0.739918 9/10 NonOverlappingTemplate
0 2 2 1 1 0 1 2 1 0 0.739918 10/10 NonOverlappingTemplate
2 1 0 2 0 0 1 2 0 2 0.534146 10/10 NonOverlappingTemplate
1 0 3 1 1 0 0 1 1 2 0.534146 10/10 NonOverlappingTemplate
1 1 0 1 1 1 0 3 2 0 0.534146 10/10 NonOverlappingTemplate
1 1 1 0 1 1 1 1 3 0 0.739918 9/10 NonOverlappingTemplate
1 3 0 0 1 2 1 0 1 1 0.534146 10/10 NonOverlappingTemplate
1 1 0 1 0 1 2 3 1 0 0.534146 10/10 NonOverlappingTemplate
2 2 1 0 0 2 1 1 0 1 0.739918 10/10 NonOverlappingTemplate
3 0 0 2 1 2 1 0 1 0 0.350485 10/10 NonOverlappingTemplate
3 1 1 2 0 2 1 0 0 0 0.350485 10/10 NonOverlappingTemplate
0 1 2 2 1 1 1 0 2 0 0.739918 10/10 NonOverlappingTemplate
1 2 1 2 0 1 0 3 0 0 0.350485 10/10 NonOverlappingTemplate
1 1 1 2 2 0 0 2 1 0 0.739918 10/10 NonOverlappingTemplate
3 1 1 0 2 0 1 0 0 2 0.350485 10/10 NonOverlappingTemplate
0 1 0 0 2 0 2 1 1 3 0.350485 10/10 NonOverlappingTemplate
1 1 2 1 0 0 2 1 0 2 0.739918 10/10 NonOverlappingTemplate
1 0 3 1 0 2 1 0 2 0 0.350485 10/10 NonOverlappingTemplate
3 3 0 1 0 0 0 2 0 1 0.122325 9/10 NonOverlappingTemplate
1 1 2 3 0 0 0 1 1 1 0.534146 10/10 NonOverlappingTemplate
1 3 1 1 0 0 3 0 1 0 0.213309 10/10 NonOverlappingTemplate
1 1 2 1 0 3 0 0 1 1 0.534146 10/10 NonOverlappingTemplate
2 1 1 1 0 1 0 0 2 2 0.739918 9/10 NonOverlappingTemplate
2 1 0 1 1 2 0 0 1 2 0.739918 9/10 NonOverlappingTemplate
0 1 3 1 2 1 1 0 0 1 0.534146 10/10 NonOverlappingTemplate
0 1 1 4 0 0 1 0 1 2 0.122325 10/10 NonOverlappingTemplate
1 1 0 2 0 2 1 1 0 2 0.739918 10/10 NonOverlappingTemplate
1 1 1 0 0 2 2 1 1 1 0.911413 10/10 NonOverlappingTemplate
1 2 1 1 1 0 1 3 0 0 0.534146 10/10 NonOverlappingTemplate
0 2 1 1 1 0 2 0 0 3 0.350485 10/10 NonOverlappingTemplate
0 0 2 1 1 2 1 1 0 2 0.739918 10/10 NonOverlappingTemplate
1 2 0 0 4 1 0 1 0 1 0.122325 10/10 NonOverlappingTemplate
0 1 2 3 0 0 2 0 0 2 0.213309 10/10 OverlappingTemplate
1 0 1 1 1 3 1 0 1 1 0.739918 10/10 Universal
1 1 0 0 0 2 2 1 1 2 0.739918 10/10 ApproximateEntropy
0 2 0 1 0 1 1 2 0 0 ---- 7/7 RandomExcursions
0 1 0 1 2 0 2 0 0 1 ---- 7/7 RandomExcursions
0 2 0 2 0 0 1 0 2 0 ---- 7/7 RandomExcursions
2 2 0 1 0 0 0 0 1 1 ---- 7/7 RandomExcursions
0 0 1 3 0 1 0 1 1 0 ---- 7/7 RandomExcursions
0 0 1 0 4 0 1 0 0 1 ---- 7/7 RandomExcursions
2 0 1 2 0 0 1 1 0 0 ---- 7/7 RandomExcursions
1 0 0 1 1 0 0 1 1 2 ---- 7/7 RandomExcursions
1 0 0 2 2 1 0 1 0 0 ---- 7/7 RandomExcursionsVariant
1 0 0 0 4 0 0 1 1 0 ---- 7/7 RandomExcursionsVariant
1 0 0 0 2 1 2 1 0 0 ---- 7/7 RandomExcursionsVariant
0 0 2 0 0 3 0 0 1 1 ---- 7/7 RandomExcursionsVariant
0 1 0 2 2 0 0 0 2 0 ---- 7/7 RandomExcursionsVariant
0 1 1 2 0 1 0 1 1 0 ---- 7/7 RandomExcursionsVariant
0 2 0 1 2 0 0 1 0 1 ---- 7/7 RandomExcursionsVariant
0 1 1 0 2 1 0 0 1 1 ---- 7/7 RandomExcursionsVariant
0 1 0 1 1 1 0 2 1 0 ---- 7/7 RandomExcursionsVariant
0 0 1 1 1 1 1 1 0 1 ---- 7/7 RandomExcursionsVariant
1 1 0 0 2 0 0 3 0 0 ---- 7/7 RandomExcursionsVariant
1 1 2 1 0 0 0 1 1 0 ---- 7/7 RandomExcursionsVariant
1 1 2 0 0 2 0 0 0 1 ---- 7/7 RandomExcursionsVariant
0 1 2 1 0 1 0 0 0 2 ---- 7/7 RandomExcursionsVariant
0 2 0 1 0 0 1 1 1 1 ---- 7/7 RandomExcursionsVariant
0 1 1 0 1 0 1 1 1 1 ---- 7/7 RandomExcursionsVariant
0 1 0 1 1 1 0 0 3 0 ---- 7/7 RandomExcursionsVariant
0 0 1 2 0 2 0 0 1 1 ---- 7/7 RandomExcursionsVariant
2 0 1 0 2 1 2 0 1 1 0.739918 10/10 Serial
1 0 2 0 0 3 2 0 2 0 0.213309 10/10 Serial
0 1 3 1 0 1 1 0 0 3 0.213309 10/10 LinearComplexity
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The minimum pass rate for each statistical test with the exception of the
random excursion (variant) test is approximately = 8 for a
sample size = 10 binary sequences.
The minimum pass rate for the random excursion (variant) test
is approximately = 6 for a sample size = 7 binary sequences.Looking at the proportion of tests passed, it’s a pass 😏 Which is interesting in that a 4 MB file has passed NIST’s STS with $H_{\infty} = 7.94$ bits/byte. We won’t use it like this though as we’re aiming for a world beating $H_{\infty} = 1 - 2^{-128}$ bits/bit.
Supplemental
Whilst the fixed length segment was folded and stacked into four pieces, we have tried our IID transformation with three pieces. And it still produces fully verified IID data as shown from our slow IID test output below:-
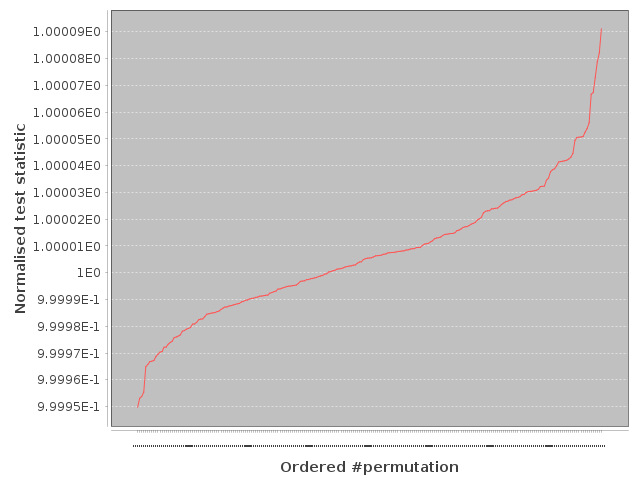
Our slow IID test of 3 stack transformation output.
So the entropy rate can be safely increased to 46 kbits per 5,831 byte segment/frame, still at $H_{\infty} = 7.9$ bits/byte. The three stack variant unfortunately fails NIST STS randomness testing by a clear margin, but that’s not the objective at this point as randomness extraction will follow. The test file (r_3-stack) is available below:-