Proving randomness
Or, how can we prove to ourselves that output from a TRNG is indeed truly random?

“It seems natural to call a chain random if it cannot be written down in a more condensed form, i.e., if the shortest program for generating it is as long as the chain itself. “ - Andrey N. Kolmogorov.
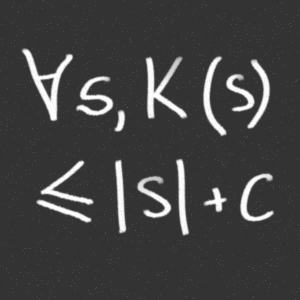 Randomness tests with only data as input can mathematically and thus conclusively prove non-randomness, but not vice versa. It is impossible to prove that a chain of numbers you’re given is truly random without further information about how they came to be. Computational indistinguishability means that a truly random sequence looks very much like a pseudo random sequence when tested within polynomial time.
Randomness tests with only data as input can mathematically and thus conclusively prove non-randomness, but not vice versa. It is impossible to prove that a chain of numbers you’re given is truly random without further information about how they came to be. Computational indistinguishability means that a truly random sequence looks very much like a pseudo random sequence when tested within polynomial time.
This is the paradigm that vexes users of all commercial TRNGs concerned about their device’s true security. A deep question thus arises from Kolmogorov’s quotation – what is the shortest program that describes your data set? Is it already as short as possible, or does GCHQ know a shorter algorithm? Or more simply, just what/who made it exactly? Where do the uncertainty/secrets truly originate?
True (Kolmogorov) random sequences possess three fundamental properties. Each of these may be taken as the basis of a definition of randomness:-
- Being typical. There are many typical sequences and that each typical sequence belongs to a reasonable majority.
- Having stability of frequencies. By definition, a binary sequence is stochastic whenever any suitably chosen subsequence of it has frequency stability.
- Being chaotic. Being chaotic signifies a complexity of structure. Then the fact that a sequence is chaotic signifies that the complexity of its beginning segments grows sufficiently fast.
Properties one and two can be achieved by pseudo random number generators. They can be tested against a specific null hypothesis ($H_0$) that they generate IID data using myriad statistical tests. Tests like Chi, Non-overlapping Template Matching Test, Maurer’s Universal Statistical Test, Parking Lot Test, etc. For each applied test, a decision or conclusion is derived that accepts or rejects $H_0$, i.e., whether the generator is (or is not) producing random looking values, based on the sequence that was produced.
Let’s test two distribution ensembles $C$ and $R$ over domain $D$, which for IID RNGs is typically the range of a byte (0 – 255) or a bit (0 - 1). $C$ is generated by a CSPRNG and $R$ is the ideal theoretical ensemble expected of a perfectly true random source. We can calculate a statistical distance between them by summing up the various differential probabilities as:-
$$ \epsilon = \Delta(n) = \frac{1}{2} \sum_{\alpha \in D} | \text{Pr}(C_n = \alpha) - \text{Pr}(R_n = \alpha) | $$
All good plain pseudo random and cryptographic RNGs will offer a negligible concrete $\epsilon$ which NIST defines as $\le 2^{-64}$, which is a miniscule 0.000000000000000000054 in English. And empirically, you’d need to take $ >340 \times 10^{36} $ samples to determine any particular $\epsilon$ at a 95% level of confidence ($Z=2, \text{in} \enspace n = \frac{Z^2}{4 \epsilon^2}$). Consequently they can’t be differentiated mathematically (in polynomial time). Even the non cryptographic Mersenne Twister (as in Python) makes a very good fist of $\epsilon$. Simply put, the distribution ensembles look the same for all intents and purposes. So far so good.
Property three is where your problem and our interest lies. Is it truly chaotic or just appears complex? The binary expansions of irrational numbers like $ \pi, e $ and $ \sqrt{2} $ are widely regarded as being perfectly pseudo random, but are nevertheless calculable and therefore predicable. Yet these constants pass all randomness tests. Indeed, they are used as test data sets to verify the tests themselves (like NIST SP 800-22, Appendix B).
They are not truly random though. The entirety of $ \pi $ can be expressed with a Kolmogorov complexity of just the following few mathematical symbols:-
$$ \pi = \sum_{0}^{\infty} \left( \frac{4}{8n+1} - \frac{2}{8n+4} - \frac{1}{8n+5} - \frac{1}{8n+6} \right) \left( \frac{1}{16} \right)^n $$
And similarly 1MB of perfectly random looking data can actually consist of only three lines of Java as:-
SecureRandom random = SecureRandom();
byte numbers[] = new byte[1_000_000];
random.nextBytes(numbers);or even less if you have access to the ChaCha20 powered Linux random number generator:-
dd if=/dev/urandom of=pseudo-random-chain bs=1M count=1Kwhich very quickly produces 1GB of pseudo random bytes that are specifically and very carefully designed to pass any and all cryptographic strength randomness tests.
So the answer to the problem of property three is that we “don’t know” and you can’t tell. Monotonic growth in apparent complexity alone just isn’t sufficient evidence to prove Kolmogorov randomness. There very well may be a program much shorter than your data set, covertly or via a cock-up operating as $ \operatorname{G}: \{0,1\}^n \to \ \{0,1\}^m $ with $m \gg n$. The data would not possess information theoretic security, and therefore would not be as secure as possible. And perhaps even predictable by sufficiently resourced actors. By it’s very definition, such a sequence could not create a one time pad.
It’s just not possible for anyone to tell what the original generator of your sample chain is if it comes out of a sealed black box .
References:-
Ref. A.N.KOLMOGOROV AND V.A.USPENSKII (Translated by Bernard Seckler), ALGORITHMS AND RANDOMNESS, THEORY PROBAB. APPL., Vol 32, No. 3.